Optics at the independent particle level

In this tutorial you will learn the first steps for calculating optical properties with Yambo. In particular we will perform optics calculations at the independent particle (IPA) level for bulk hexagonal boron nitride (hBN).

Requirements

  • hBN folder: download and extract hBN.tar.gz from the Tutorial files page

  • the SAVE folder (present in hBN/YAMBO)

  • yambo executable

  • gnuplot for plotting spectra

The dielectric function in the long-wavelength limit at the independent particle level (RPA without local fields) is essentially given by the following:

(1)\[\epsilon_{\alpha, \alpha}(\omega)= 1+\frac{16 \pi}{\Omega} \sum_{c, v} \sum_{\mathbf{k}}\frac{1}{E_{c \mathbf{k}}-E_{v \mathbf{k}}} \frac{\left|\left\langle v \mathbf{k}\left|\mathbf{p}_{\alpha}+\mathrm i\left[V^{\mathrm{NL}}, \mathbf{r}_{\alpha}\right]\right| c \mathbf{k}\right\rangle\right|^{2} }{\left(E_{c \mathbf{k}}-E_{v \mathbf{k}}\right)^{2}-(\omega + i \gamma)^{2}}\]

In practice, Yambo does not use this expression directly but solves the Dyson equation for the susceptibility \(\chi\) (see tutorial on local fields).

We will use bulk hBN as an example, so download and unpack the files and then go to the YAMBO directory:

$ cd hBN/YAMBO

Remember that the first thing to do is to initialize the SAVE folder (or check if it has been already initialized):

$ ls SAVE/ndb.*
No such file or directory
$ yambo
[...]
$ ls
SAVE  l_setup  r_setup
$ ls SAVE
SAVE/ndb.gops  SAVE/ndb.kindx

Input file and parameters

We want to perform a IPA optical spectrum calculation: the option to generate the input file is -optics c (or -o c). Let’s also add the option to choose the input file name:

$ yambo -F yambo.in_IP -o c

Tip

Remember the yambo -h command to print all the available options.

Important

In the input file the independent particle approximation for the optics is indicated by

Chimod= "IP"                     # [X] IP/Hartree/ALDA/LRC/PF/BSfxc

Optics runlevel

For optical properties we are interested just in the long-wavelength limit \(\mathbf{q} \to 0\). This always corresponds to the first \(\mathbf{q}\)-point in the set of possible \(\mathbf{q} =\mathbf{k} - \mathbf{k}'\) points.

Set the following input variables in yambo.in_IP to:

 % QpntsRXd   
  1 | 1 |                    # [Xd] Transferred momenta
 %
 ETStpsXd= 1001              # [Xd] Total Energy steps

Setting the range of the variable QpntsRXd to 1 | 1 selects just the first \(\mathbf{q}\).

ETStpsXd instead selects the number of calculated frequencies: a large value ensures a smooth spectrum.

We can now run the calculation, specifying a job label using the -J option:

$ yambo -F yambo.in_IP -J Full
View l-Full_optics_dipoles_chi
 <---> [01] MPI/OPENMP structure, Files & I/O Directories
 <---> MPI assigned to GPU : 0
 <---> [02] CORE Variables Setup
 <---> [02.01] Unit cells
 <---> [02.02] Symmetries
 <---> [02.03] Reciprocal space
 <---> [02.04] K-grid lattice
 <---> Grid dimensions      :   6   6   2
 <---> [02.05] Energies & Occupations
 <---> [03] Transferred momenta grid and indexing
 <---> [04] Dipoles
 <---> [04.01] Setup: observables and procedures
 <---> [DIP] Database not correct or missing. To be computed
 <---> [x,Vnl] computed using 4 projectors
 <02s> R V P [g-space] |########################################| [100%] --(E) --(X)
 <02s> [WARNING] [r,Vnl^pseudo] included in position and velocity dipoles.
 <02s> [WARNING] In case H contains other non local terms, these are neglected
 <02s> [05] Optics
 <02s> [LA] SERIAL linear algebra
 <02s> [X-CG] R(p) Tot o/o(of R):    5499   52992     100
 <02s> Xo@q[1] |########################################| [100%] --(E) --(X)
 <02s> [06] Timing Overview
 <02s> [07] Memory Overview
 <02s> [08] Game Over & Game summary

Note

Yambo runs the calculation when there are no lowercase options after yambo.

When the calculation has finished you should see these files:

$ ls
 Full  SAVE  yambo.in_IP  r_setup  l_setup  l-Full_optics_dipoles_chi
 o-Full.eel_q1_ip  o-Full.eps_q1_ip  r-Full_optics_dipoles_chi

Let’s take a moment to understand what Yambo has done inside the Optics runlevel:

  1. Compute the \([\mathbf{r}, V^\mathrm{NL}]\) term

  2. Read the wavefunctions from disc [WF]

  3. Compute the dipoles, i.e. matrix elements of \(\mathbf{p}\)

  4. Write the dipoles to disk as Full/ndb.dip* databases. You can check this from the report file:

$ grep -A16 "WR" r-Full_optics_*
grep output
[WR./Full//ndb.dipoles]---------------------------------------------------------
 Brillouin Zone Q/K grids (IBZ/BZ)                :   14   72   14   72
 RL vectors                                       :  1491 [WF]
 Fragmentation                                    : yes
 Electronic Temperature                           :  0.000000 [K]
 Bosonic    Temperature                           :  0.000000 [K]
 DIP band range                                   :    1  100
 DIP band range limits                            :   8   9
 DIP e/h energy range                             : -1.000000 -1.000000 [eV]
 RL vectors in the sum                            :  1491
 [r,Vnl] included                                 : yes
 Bands ordered                                    : yes
 Direct v evaluation                              : no
 Approach used                                    : G-space v
 Dipoles computed                                 : R V P [G-space]
 Wavefunctions                                    : Slater exchange(X)+Perdew & Zunger(C)
- S/N 003471 ---------------------------------------------- v.05.03.00 r.23927 -

$ grep -A16 "WR" r-Full_optics_*
grep output
[WR./Full//ndb.dip_iR_and_P]
Brillouin Zone Q/K grids (IBZ/BZ):  14   72   14   72
RL vectors                   (WF): 1491
Electronic Temperature        [K]: 0.0000000
Bosonic    Temperature        [K]: 0.0000000
X band range           :   1  100
RL vectors in the sum  : 1491
[r,Vnl] included       :yes
...

  1. Finally, Yambo computes the non-interacting susceptibility \(\chi\) for this \(\mathbf{q}\), and writes the dielectric function inside the o-Full.eps_q1_ip file for plotting

Important

If yambo is computing new databases you will see WR. at the corresponding runlevel in the report file. If yambo finds a compatible database, this will be read and you will see RD. in place of WR..

This is useful to check wheter yambo is actually computing the database, especially after you have changed some input variables.

Note on the energy cutoff

The previous calculation used all the G-vectors in expanding the wavefunctions, up to 1491 (~1016 components). This corresponds roughly to the cut off energy of 40 Ry we used in the DFT calculation.

Generally, however, we can use a smaller value. We use the verbosity to switch on this variable:

$ yambo -F yambo.in_IP  -V RL -o c

Change the value of FFTGvecs and also its unit from RL (number of G-vectors) to Ry (energy in Rydberg):

FFTGvecs= 6 Ry  # [FFT] Plane-waves

Save the input file and launch the code again with a new -J flag to avoid reading the database from before:

$ yambo -F yambo.in_IP -J 6Ry

The result will be printed in the file o-6Ry.eps_q1_ip.

Caution

In general the best practice is to keep the value of FFTGvecs at its default (maximum) value.

Plotting the output

To plot the result in o-Full.eps_q1_ip file type:

$ gnuplot
gnuplot> plot "o-Full.eps_q1_ip" w l

The figure below also shows the results with lower energy cutoff. If you also did this calculation you can add the plot on top of the previous one with replot "o-6Ry.eps_q1_ip" w p.

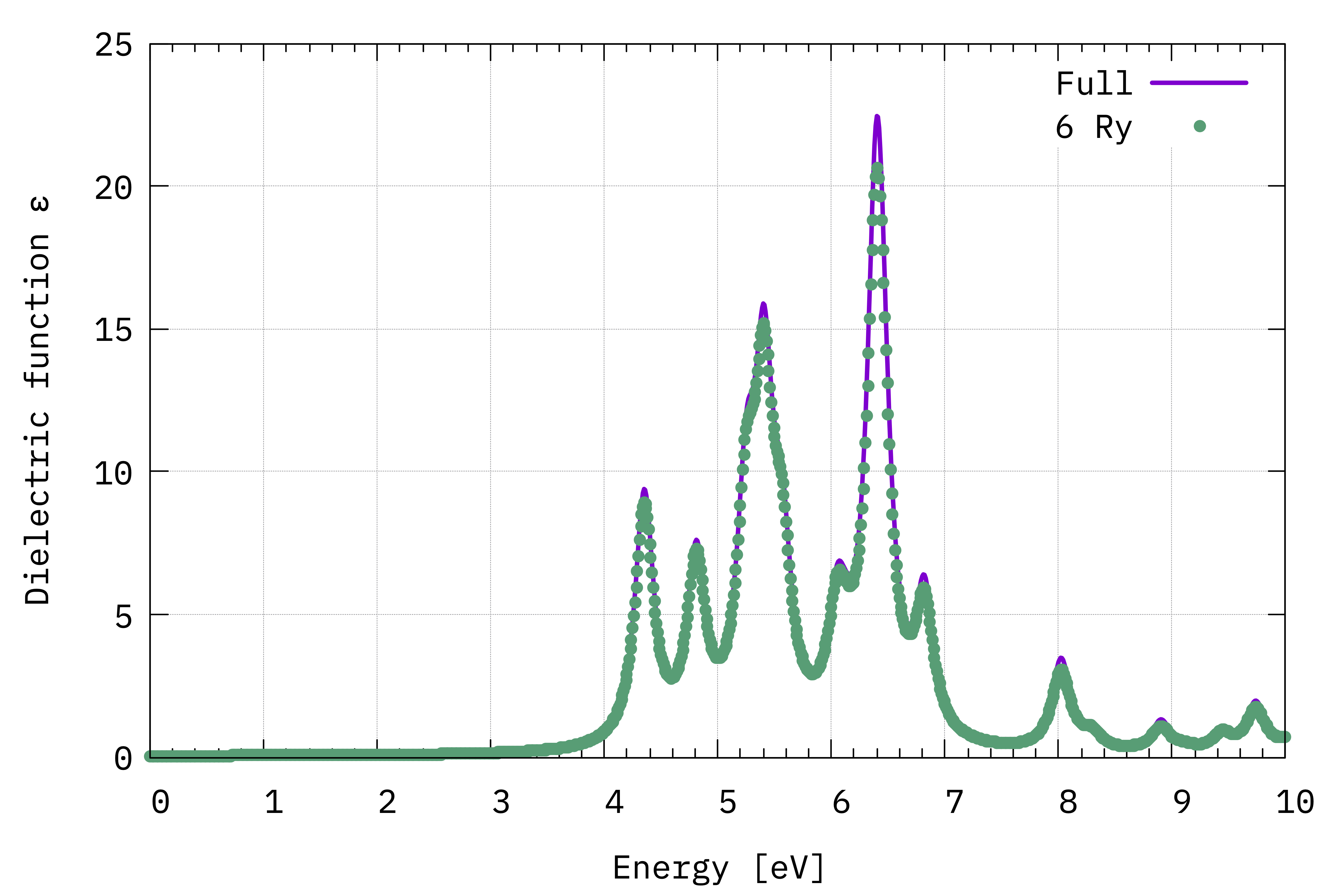
../../_images/hBN-IPA-eps_Full-vs-6Ry.png

Comparison between the IPA dielectric functions in the long-wavelenght limit, i.e. \(\Im(\varepsilon_{\alpha,\alpha}(\omega))\) (Eq.(1)), computed with the total number available G-vectors (Full) and a cutoff value of 6 Ry.

Note

In this case the direction of the electric field (i.e. \(\alpha,\alpha\)) is the one of the lattice vector \(\boldsymbol{\mathrm{a}}\) of the unit cell – which is also parallel to the \(x\) axis – because in the input file we have

% LongDrXd
 1.000000 | 0.000000 | 0.000000 |        # [Xd] [cc] Electric Field
%

Important

We can see that there is very little difference between the two spectra. This highlights an important point in calculating excited state properties: generally, fewer G-vectors are needed than what are needed in DFT calculations. However we suggest to never change the value of FFTGvecs (unless you have very limited memory, in which case carefully check how changing this value affects the results).

Regarding the spectrum itself, the first peak occurs at about 4.4 eV. This is consistent with the minimum direct gap reported by Yambo: 4.28 eV. The comparison with experiment (not shown) is very poor however. This is because in most materials more advanced techniques than IPA/RPA are needed.

q-direction

../../_images/hBN-bulk-3x3.png

Atomic structure of bulk hBN (\(z \parallel c\) is the stacking direction).

Now let’s do the calculation for the \(\epsilon_{z,z}(\omega)\) component of the dielectric tensor. To do so we modify LongDrXd in the input file

$ yambo -F yambo.in_IP -V RL -o c
...
% LongDrXd
0.000000| 0.000000 | 1.000000 |        # [Xd] [cc] Electric Field
%
...

and run the calculation again

$ yambo -F yambo.in_IP -J Full

This time yambo reads from the Full folder, so it does not need to compute the dipole matrix elements again and the calculation is faster. Let’s plot the result:

$ gnuplot
gnuplot> plot "o-Full.eps_q1_ip" t "q || x-axis" w l,"o-Full.eps_q1_ip_01" t "q || z-axis" w l
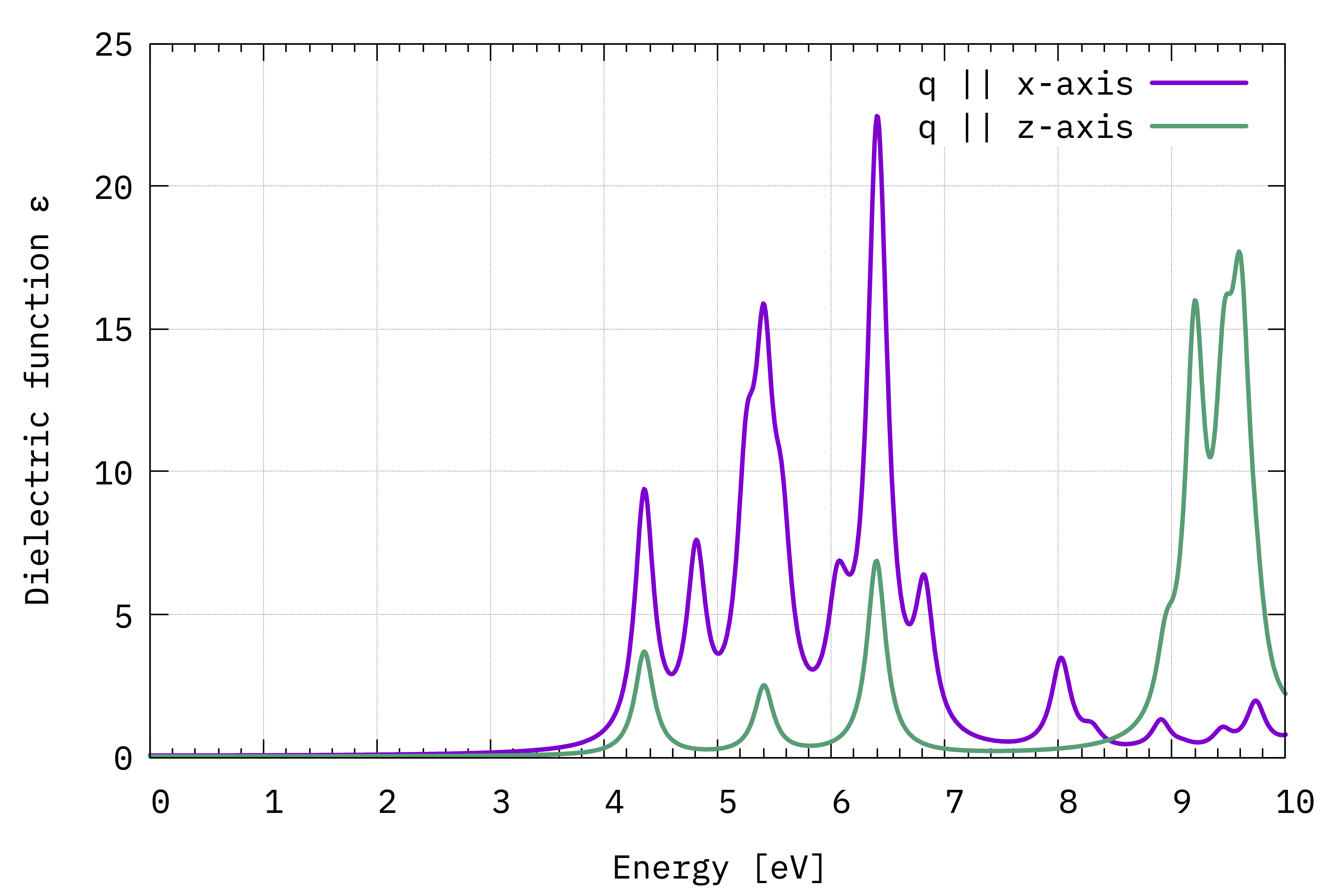
../../_images/hBN-IPA-eps_x-vs-z.png

Comparison between \(\Im(\varepsilon_{x,x}(\omega))\) and \(\Im(\varepsilon_{z,z}(\omega))\) (Eq.(1)).

The absorption is suppressed in the stacking direction. As the interplanar spacing is increased, we would eventually arrive at the absorption of the BN sheet (see local fields tutorial).

Non-local commutator

Last, we show the effect of switching off the non-local commutator term (the term with \(V^\mathrm{NL}\) in Eq. (1)) due to the pseudopotential.

As there is no option to do this inside yambo, you need to hide the database file, for example renaming it like this:

$ mv SAVE/ns.kb_pp_pwscf SAVE/ns.kb_pp_pwscf_OFF

Then open the input file and modify it back to do the calculation along the \(q \parallel (1 0 0)\) direction

 % LongDrXd
 1.000000  | 0.000000 |  0.000000  | 
 %

and launch yambo with a different -J label:

$ yambo -F yambo.in_IP -J Full_NoVnl

Important

Note the warning in the log:

<---> [WARNING] [r,Vnl^pseudo] not included in position and velocity dipoles

which also appears in the report file r-Full_NoVnl_optics_dipoles_chi as

[WR./Full_NoVnl//ndb.dipoles]----------------------------------------------------
 ...
 [r,Vnl] included                                 : no
 ...

Plotting the result we see that the difference is small:

$ gnuplot
gnuplot> plot "o-Full.eps_q1_ip" w l t "w/ Vnl", "o-Full_NoVnl.eps_q1_ip" w p t "no Vnl"
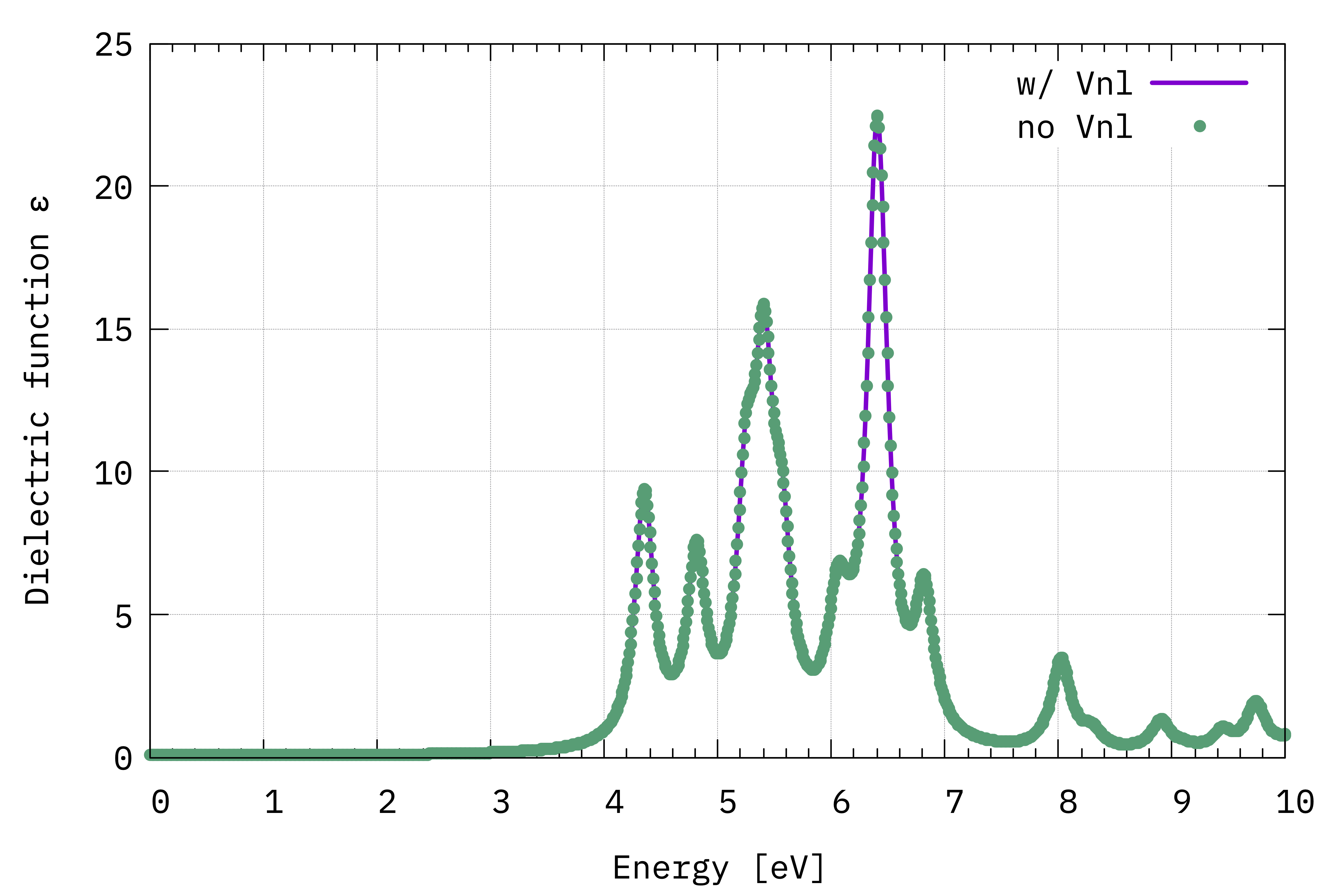
../../_images/hBN-IPA-eps_w-vs-noVnl.png

Comparison between \(\Im(\varepsilon_{x,x}(\omega))\) computed with and without the \(V^{\mathrm{NL}}\) term (Eq.(1)).

Tip

When you have a large sistem, either with more projectors in the pseudopotential or more k-points, the inclusion of \(V^\mathrm{NL}\) can make a huge difference in the computational load. So it is always worth checking to see if these terms are important for your system.