BSE on MoS2: solvers

In this tutorial we will focus on the solution of the BSE equation. We will use 2D MoS2 as an example system.

Requirements

  • SAVE folder of 2D MoS2: download and extract the correct tar.gz file mentioned in the main school page.

  • (optional) directory containing quasiparticle databases from GW calculation and precomputed RPA screening (also provided in tar.gz file).

  • yambo executable

  • python in order to use some of the provided scripts

  • gnuplot (optional) for plotting some of the results

Yambo is run on top of DFT results, in this case from the code Quantum ESPRESSO (QE). You can find a QE pre-computed saved directory in 00_QE-DFT.

The “step 0” of every calculation is converting this directory to yambo-readable format. This is already done for you and in 01_BSE_Hamiltonian (where you will start the tutorial) you can already find a Yambo SAVE folder.

You can also try generate and initialize this folder yourself by running the yambo-to-QE interface, but you need to be familiar with the concepts related to the SAVE folder and handling files with Yambo.

The SAVE directory contains:

  • crystal lattice information in real and reciprocal space

  • pseudopotential information

  • DFT-computed electron energies

  • DFT-computed electron wavefunctions

These data are the DFT starting point to the many-body perturbation theory simulations.

In addition, while a BSE calculation can be run on top of DFT results, from a theoretical point of view this should be done on top of a GW calculation to maintain consistency of methods used. For this tutorial, you can use the databases for quasiparticle energies and RPA screening already calculated during the GW-HPC tutorial on monolayer MoS2.

For your convenience, the directory containing those databases, called GW_bnds, is already precomputed and provided in 01_BSE_Hamiltonian.

The GW_bnds directory contains:

  • ndb.QP database with quasiparticle energies

  • ndb.pp* databases with static RPA microscopic dielectric function

  • ndb.RIM, ndb.cutoff databases concerning the Coulomb potential integration in 2D (since we are dealing with a 2D system).

See also

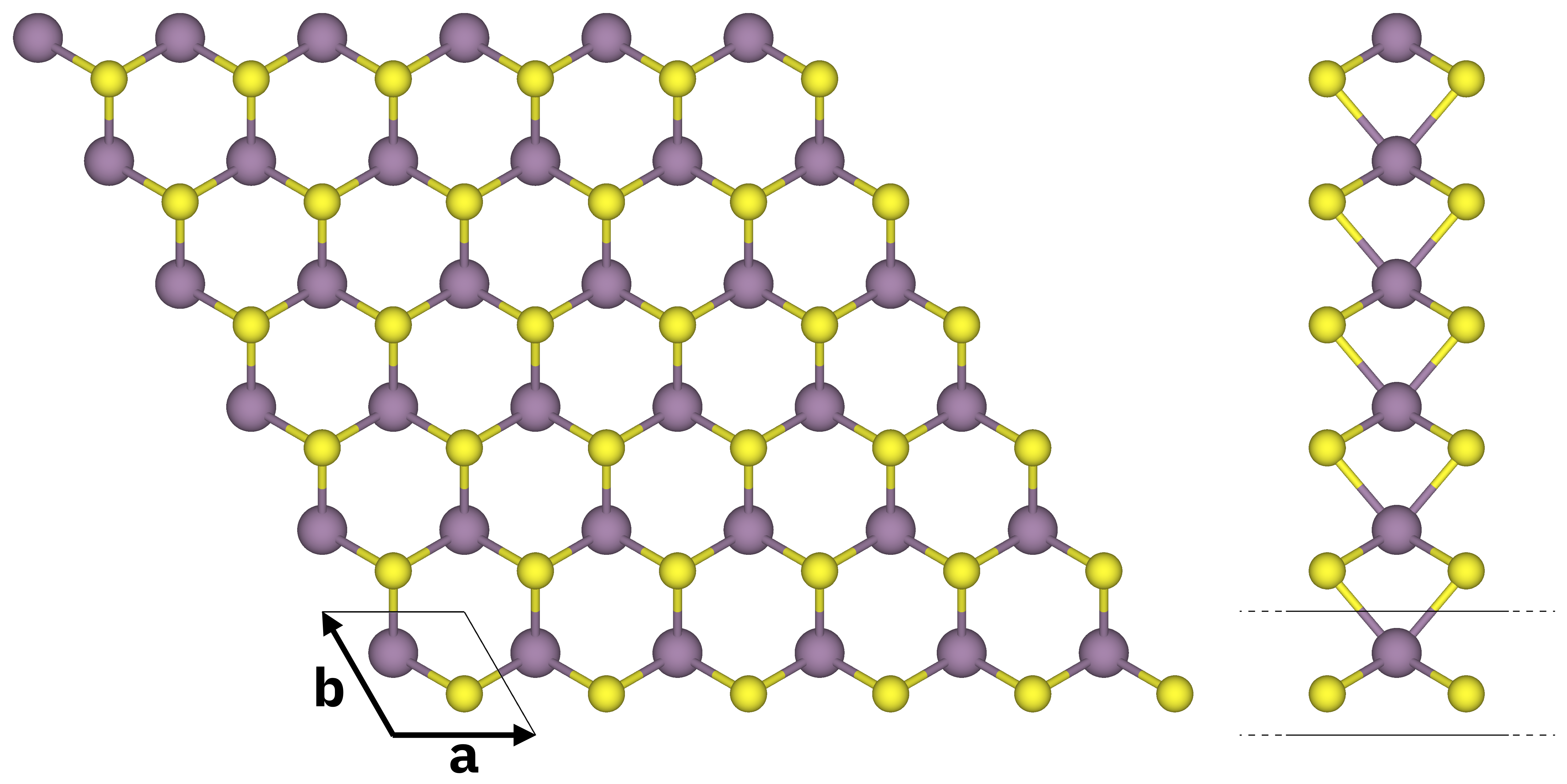
../../_images/MoS2-2D-6x6_top-side.png

Atomic structure of monolayer MoS\(<sub>2</sub>\) (top and side views). S atoms in yellow, Mo atoms in purple. The solid black lines mark the unit cell.

The target quantity in a Bethe-Salpeter calculation is the macroscopic dielectric matrix \(\epsilon_{M}\). The following quantities/steps are needed to obtain \(\epsilon_{M}\):

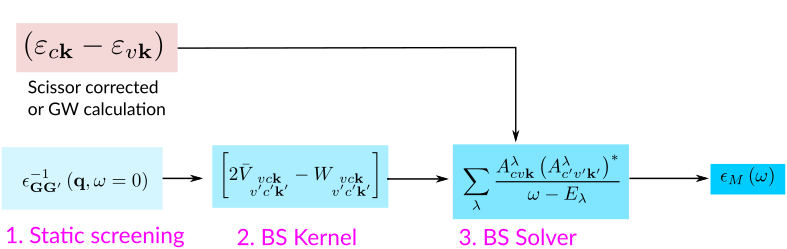
../../_images/Scheme1b.png

Build the excitonic Hamiltonian:

You can find the files needed to start the tutorial in the folder 01_BSE_Hamiltonian.

To solve the Bethe–Salpeter equation (BSE), it is customary to rewrite it in the basis of transitions between valence and conduction states. In this representation, the problem takes the form of an eigenvalue equation for an effective two-particle Hamiltonian. For a non–spin-polarized system and in the optical limit \(q=0\), the matrix elements of the two-particle Hamiltonian are given by:

(1)\[\begin{split}H_{\substack{cvk\\c'v'k'}} = (\epsilon_{ck}-\epsilon_{vk})\delta_{vv'}\delta_{cc'}\delta_{kk'}+(f_{ck}-f_{vk})\Big[2\hat{V}_{\substack{cvk\\c'v'k'}}-W_{\substack{cvk\\c'v'k'}} \Big]\end{split}\]

where \(vck\) indicates the pair of quasiparticle states \(vk\) and \(ck\) (that is, an electron-hole transition from the valence band to the conduction band with momentum \(\mathbf{k}\)). Quasiparticle energies are either calculated from a previous GW calculations or approximated by the Kohn-Sham energies (calculated at DFT level) corrected through a scissor operator.

The first term on the RHS is the quasiparticle energy differences (diagonal only). The second term is the kernel which is the sum of the electron-hole exchange part \(V\) – which stems from the Hartree potential and has a repulsive effect – and the electron-hole attraction part \(W\) – which stems from the screened exchange potential: this term is attractive and responsible for the binding of electron-hole pairs. The electron-hole interaction kernel both shifts (diagonal contributions) and couples (off-diagonal contributions) the quasiparticle energy differences.

The kernel contributions are built up by calculating the following expressions:

(2)\[\begin{split}W_{\substack{cv{\bf k}\\c'v'{\bf k}'}} = \frac{1}{\Omega}\sum_{GG'}v({\bf q}+{\bf G}')\epsilon^{-1}_{{\bf G}{\bf G}'}({\bf q})\langle v'{\bf k}' | e^{-i({\bf q}+{\bf G}'){\bf r}}| v{\bf k} \rangle \langle c {\bf k} | e^{i({\bf q}+{\bf G}){\bf r}} |c'{\bf k}' \rangle \delta_{{\bf q},{\bf k}-{\bf k}'}\end{split}\]
(3)\[\begin{split}\hat{V}_{\substack{cv{\bf k}\\c'v'{\bf k}'}} = \frac{1}{\Omega}\sum_{G \neq 0}v({ G})\langle v'{\bf k}' | e^{-i({\bf q}+{\bf G}'){\bf r}}| c{\bf k}' \rangle \langle c {\bf k} | e^{i({\bf q}+{\bf G}){\bf r}} |v{\bf k}' \rangle\end{split}\]

Here \(\epsilon^{-1}_{{\bf G}{\bf G}'}\) is the inverse of the dielectric screening matrix which was evaluated at RPA level (see local fields tutorial)

Yambo input file

We now generate the input file needed to build the BSE kernel. This is done using the yambo executable with the following command-line instruction:

$ yambo -o b -X p -k sex -r -F bse.in -V all -J GW_bnds

Tip

Type yambo -h for the full list of options.

Depending on the machine you are running on, you might want to this in an interactive node.

With these options we generate an input file where for a Bethe-Salpeter optics calculation (-o b), using the RPA screening from a plasmon-pole calculation (-X p) and using the Hartree-Screened exchange kernel (-k sex). We also add a truncation of the Coulomb potential which is useful for 2D systems (-r). In addition, we want to set up explicitly the parameters for parallel runs and for the inclusion of quasiparticle energies (separately, they are turned on with -V qp and -V par, but here we turn everything on with -V all).

You can now inspect the input file bse.in and try to familiarize with some of the parameters. The input will come with default values for many parameters that we might need to change.

However, we do not need to change the parameters related to the RPA screening, because they are automatically read from the precomputed database that we passed with -J GW_bnds (see the GW tutorial for those).

Let us quickly recall the other parameters below.

Runlevels

optics                           # [R] Linear Response optical properties
ppa                              # [R][Xp] Plasmon Pole Approximation for the Screened Interaction
rim_cut                          # [R] Coulomb potential
bse                              # [R][BSE] Bethe Salpeter Equation.
dipoles                          # [R] Oscillator strenghts (or dipoles)
em1d                             # [R][X] Dynamically Screened Interaction

These flags tell Yambo which parts of the code should be executed. Each runlevel enables its own set of input variables. Here we have:

  • optics: This is a calculation of optical properties

  • bse: With the bse kernel

  • dipoles: Dipoles are needed to build the kernel

  • em1d and ppa: even if the BSE kernel just needs a static screening, we can use the previously calculated screening at plasmon-pole level as it contains the static limit at \(\omega=0\).

Bethe-Salpeter Hamiltonian

The relevant input variables to be set are:

BSENGexx=  20 Ry    # [BSK] Exchange components
BSENGBlk=  5  Ry    # [BSK] Screened interaction block size [if -1 uses all the G-vectors of W(q,G,Gp)]
% BSEBands
 23 | 30 |          # [BSK] Bands range 
%

  • BSENGexx: cutoff for bare exchange interaction \(V\) for the summations over reciprocal lattice vectors

  • BSENGBlk: cutoff for screened interaction \(W\) for the summations over reciprocal lattice vectors

  • BSEBands: range of quasiparticle states – identified by their band indices - that define the basis of electron–hole pairs used to describe excitonic states in the chosen energy window.

In our case, since the system has 26 occupied bands, we select bands 23–30, corresponding to four valence and four conduction bands. This choice leads to a total of 4×4=16 valence–conduction band pairs.

For each of these band pairs, all k-points available from the underlying DFT calculation are included. With a 18×18×1 Monkhorst–Pack grid, this corresponds to 324 total k-points in the Brillouin zone.
As a result, the excitonic Hamiltonian is represented in a basis of 16×1296=5184 valence–conduction–k (vck) pairs (dimension of the matrix).

Note

The numerical values chosen for these three parameters should be determined through systematic convergence studies.

RPA screening and Coulomb interaction

These parameters should be automatically filled in because they are read from the databases inside GW_bnds (see the GW tutorial for information).

Quasiparticle energies

KfnQPdb= "E < GW_bnds/ndb.QP"

  • KfnQPdb: with this string, we tell Yambo to look for the database ndb.QP that contains quasiparticle energies from a previous GW calculations. These will be now included in the BSE run.

Parallelization parameters

Moreover, we need to set the variables referred to the parallelism:

BS_CPU= "8 1 2"        
BS_ROLEs= "k eh t"

For this run, we will parallelize the BSE kernel over kpoints and in transition space. Different schemes may work best for different system sizes.

The additional parallelization parameters for dipoles and RPA response function are not used since we already calculated them, and the code will simply load the databases (see the GW tutorial for information).

We are ready to run the kernel calculation you can find and inspect the script run_bse.sh already provided, and submit it when you are satisfied.

In the report r-*_optics_dipoles_bse the information relative to this runlevel are reported under the section:

[05] Bethe Salpeter Equation @q1
================================

Take some time to inspect the log and the report. For example try to find where the input parameters are reported, the dimension of the two-particles Hamiltonian and if these match your expectations.

This run does not produce any human readable output. The kernel is stored in a database in the output BSE directory:

BSE/ndb.BS_Q1

Solve the excitonic Eigenvalue Problem

Now we move in the next directory for the diagonalization of the BSE Hamiltonian:

$ cd ../02_BSE_diagonalization

The eigenvalue equation reads:

(4)\[\begin{split}\sum_{c'v'k'}H_{\substack{cvk\\c'v'k'}} A^\lambda_{c'v'k'}=E^\lambda A^\lambda_{cvk}\end{split}\]

From the solution of the eigenvalue problem it is then possible to build the macroscopic dielectric function, from which the absorption and electron energy loss (EELS) spectra can be computed.

Those are obtained from the eigenvalues \(E^\lambda\) (excitonic energies) and eigenvectors \(A^\lambda_{cvk}\) (exciton composition in terms of electron-hole pairs) of the two-particles Hamiltonian:

(5)\[\epsilon_{M}(\omega) = 1-\lim_{q\rightarrow 0}\frac{8\pi}{|{\bf q}|^2\Omega} \sum_{vck}\sum_{v'c'k'} \langle v{\bf k-q} | e^{-i{\bf qr}} | c {\bf k} \rangle \langle c'{\bf k'} | e^{i{\bf qr}} | v' {\bf k'-q} \rangle \sum_{\lambda}\frac{A^\lambda_{cvk} (A^\lambda_{c'v'k'})^*}{\omega-E_\lambda}\]

Here you will find a new submission script named run_bse_diago.sh.

First, we link the previously calcaulted databases into the current directory, so that they are available:

ln -s ../01_BSE_Hamiltonian/SAVE .
ln -s ../01_BSE_Hamiltonian/BSE .
ln -s ../01_BSE_Hamiltonian/GW_bnds .

Now we will explore three different ways to solve the excitonic matrix, namely:

  1. a direct diagonalization

  2. the iterative haydock solver

  3. the iterative slepc solver

We will update the bse input in three different ways for this. Therefore, it is useful to copy the bse.in file from the previous step in the current directory, initially renaming it as bse_haydock.in and then directly add the variables relative to the solver.

$ cp ../01_BSE_Hamiltonian/bse.in bse_haydock.in

We need to add a new runlevel at the beginning of the file as below:

[...]
optics                           # [R] Linear Response optical properties
ppa                              # [R][Xp] Plasmon Pole Approximation for the Screened Interaction
rim_cut                          # [R] Coulomb potential
bse                              # [R][BSE] Bethe Salpeter Equation.
dipoles                          # [R] Oscillator strenghts (or dipoles)
bss                              # [R] BSE solver
[...]

Add the variables relative to the specific solver (Haydock in this case).

[...]
BSSmod= "h"                      # [BSS] (h)aydock/(d)iagonalization/(s)lepc/(i)nversion/(t)ddft`
BSHayTrs=0.010000               # [BSS] Relative [o/o] Haydock threshold. Strict(>0)/Average(<0)
[...]

The Haydock solver is an iterative method based on Lanczos chains. It is the fastest algorithm to obtain optical spectra, but eigenvalues and eigenvectors of the excitonic Hamiltonian are not accessible.

The following variables govern the details of the absorption spectrums: energy range, peak broadening, energy points and polarization direction of absorbed optical electric field.

% BEnRange
  1.00000 | 5.00000 |         eV    # [BSS] Energy range
%
% BDmRange
 0.0500000 | 0.0500000 |         eV    # [BSS] Damping range
%
BEnSteps= 500                    # [BSS] Energy steps
% BLongDir
 1.000000 | 1.000000 | 0.000000 |        # [BSS] [cc] Electric Field versor
%

The second method we want to adopt is the full diagonalization of the excitonic Hamiltonian. This is the slowest algorithm, and it provides access to all eigenvalues and eigenvectors.

Note anyway that usually in practical calculations only a fraction of the eigenvalues is significant to determine the optical properties of the material.

Let us create a different input by copying bse_haydock.in to bse_diago.in

$ cp bse_haydock.in bse_diago.in

In the new file, we set the variable

BSSmod= "d"                      # [BSS] (h)aydock/(d)iagonalization/(s)lepc/(i)nversion/(t)ddft`

Finally, the last method is the SLEPC. We create a third input for this:

$ cp bse_haydock.in bse_slepc.in

We now set the following lines in the new file:

BSSmod="s"    # [BSS] (h)aydock/(d)iagonalization/(s)lepc/(i)nversion/(t)ddft`
BSSNEig=10    # [SLEPC/DIAGO] Number of eigenvalues to compute
WRbsWF                        # [BSS] Write to disk excitonic the WFs

SLEPC is a library implementing iterative schemes based on Krylov-Schur or Jacobi-Davidson methods (the default setting is Krylov-Schur).

  • BSSNEig: this variable indicates the requested number of eigenvalues (and eigenvectors)

We also have an additional variable that is not related to slepc but works only when computing eigenvectors.

  • WRbsWF: (note that this variable is already present in the input but needs to be uncommented) It writes the BSE eigenvectors to disk. These are needed for post-processing purposes (such as plotting the exciton wavefunction in real space) and will be used in the following.

The script run_bse_diago.sh will run in sequence the three calculations related to the inputs we have prepared.

Now, if everything works and we check inside the absorption_* directories, we will find the relative output o-* output files.

$ ls absorption_*/o-*

These files contain the the absorption spectra of the system, computed using the diagonalized Hamiltonian.

The first column contains the energy range, and the second one the values of the imaginary part of the dielectric function (actually, since this is a 2D system, it really contains the 2D polarizability which is related to \(\varepsilon_2\) and is the physically meaningful quantity in this case).

We can compare the three absorption spectra by plotting them with gnuplot, for example via script like plotbse.gnu given below:

### Terminal
set terminal qt persist enhanced font "Helvetica,12"

### Files
file_h = "absorption_haydock/o-absorption_haydock.alpha_q1_haydock_bse"
file_d = "absorption_diago/o-absorption_diago.alpha_q1_diago_bse"
file_s = "absorption_slepc/o-absorption_slepc.alpha_q1_slepc_bse"

### Axes & tics
set xrange [1:5]
set xlabel "Energy (eV)"
unset ytics
set ylabel "Optical absorption (arb. units)"
set border lw 1.5

### Line styles
set style line 1 lc rgb "#000000" lw 2      # haydock
set style line 2 lc rgb "#d62728" lw 2 dt 2 # diago
set style line 3 lc rgb "#1f77b4" lw 2      # slepc

### Legend
set key top right spacing 1.2

### Plot
plot \
    file_h u 1:2 w l ls 1 t "haydock (iterative - only spectra)", \
    file_d u 1:2 w l ls 2 t "full diagonalization (lapack)", \
    file_s u 1:2 w l ls 3 t "slepc (iterative)"

And the result is the following.

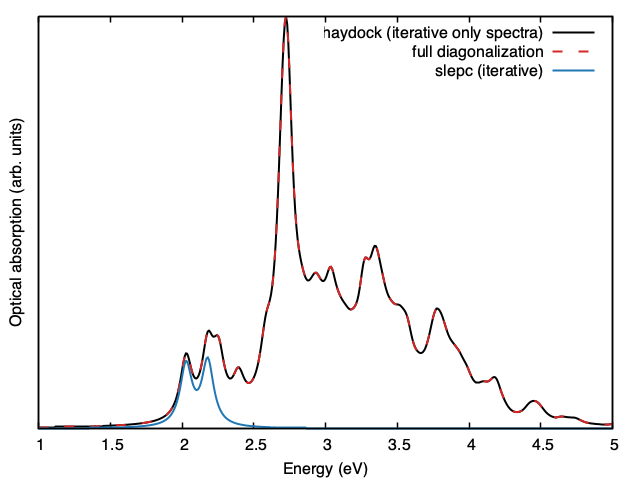
../../_images/MoS2-2D-abs.png

BSE optical absortion spectra of monolayer MoS2 obtained with three different diagonalization schemes.

This spectra are far from being numerically converged, but we still see the main excitonic features of MoS2: two starting peaks at low energy (A and B exciton - the energy difference between them depends on the strength of spin-orbit interaction) and a large resonance at higher energy, above the quasiparticle band gap.

Furthermore, we see how the haydock and diago solutions basically coincide. The slepc solution, given that we used only the first 10 states, will cut the spectrum off when they run out: here we see only the first two peaks.

Note

We should study the slepc solver more. Try to increase BSSNEig and replotting to check how it gradually reproduces a larger part of the full spectrum. Typically, you only need the spectrum in the low-energy window, and you don’t need to include many eigenvalues. If you don’t know where to start, try with 10% of the total size of the BSE kernel, which is usually both very fast and enough.

Now check the timings of the three methods from the report files:

$ grep "Timing   " absorption_*/r-*

Clearly, there is a large difference between the full diagonalization and the iterative solvers.

Postprocessing: plotting the exciton wavefunction in real space

The wavefunction \(\Psi\)corresponding to the exciton with state index \(\lambda\) is constructed by linear combination of the electron and hole Bloch functions \(\phi\) via the excitonic eigenvector coefficients:

\[\Psi_\lambda (\mathbf{r}_e,\mathbf{r}_h) = \sum_{cvk} A^\lambda_{cvk} \phi_{vk}(\mathbf{r}_h)^*\phi_{ck}(\mathbf{r}_e)\]

Here, \(\mathbf{r}_e\) and \(\mathbf{r}_h\) denote the electron and hole positions, respectively. It is not possible to fully visually represent this function because it depends on six variables. However, we can simplify it by fixing the hole at a certain chosen position (\(\mathbf{r}_0\)) and plotting the resulting function of the electron position only (we plot the intensity which is real):

\[N_\lambda (\mathbf{r}_e) = |\Psi_\lambda (\mathbf{r}_e,\mathbf{r}_h=\mathbf{r}_0)|^2 \]

You can understand the meaning of \(N_\lambda(\mathbf{r}_e)\) as the conditioned probability of finding an electron at position \(\mathbf{r}_e\) given that the hole is fixed at \(\mathbf{r}_0\) for electron-hole state \(\lambda\).

Tip

How to choose \(\mathbf{r}_0\) in a meaningful way? This in general depends on what you want to visualize, but a good strategy is to fix the hole in the most “physically sound” position: this would be the position the most important valence orbital contributing to exciton \(\lambda\) (i.e. the \(\phi_{vk}\) for which \(A^\lambda_{cvk}\) is maximum) has a maximum in intensity.

We will use the postprocessing executable ypp for this.

Tip

You can do this also with Yambopy.

Todo

Add link to yambopy tutorial.

First of all, create symbolic links in this folder for all the previously computed database folders: SAVE, GW_bnds, BSE, and absorption_slepc: the latter one contains the database ndb.BS_diago_Q1 with the exciton coefficients \(A^\lambda_{cvk}\).

Let us now analyse the exciton energies and their optical oscillator strengths (i.e., peak intensities in the spectrum).

Type

ypp -e s -J absorption_slepc,BSE,GW_bnds

Attention

You may need open an interactive session to run ypp. In this case remember to load the executables and pay attention to any run requirements.

You should obtain an output file ending in *_E_sorted. Open it:

[...]
# Atom 1 with Z 42 [cc]:-0.295004043E-8   3.40641356      0.00000000
# Atom 1 with Z 16 [cc]:  2.95004058      1.70320678      2.93654299
# Atom 2 with Z 16 [cc]:  2.95004058      1.70320678     -2.93654299
#
#    Maximum Residual Value =  0.86686E-01
#
#    E [ev]             Strength           Index
#
     2.0163708         0.66523766E-10      1.0000000
     2.0171168         0.12820390E-10      2.0000000
     2.02876091        0.902098060         3.00000000
     2.02876735        0.857971907         4.00000000
     2.1630719         0.53834254E-09      5.0000000
     2.1630721         0.60582754E-10      6.0000000
     2.17986917        0.913443565         7.00000000
     2.17987561         1.00000000         8.00000000
     2.2404346         0.34227418E-09      9.0000000
     2.24088478        0.340123241E-8      10.0000000
[...]

Here we find the energies of the 10 exciton states we computed in the previous section with slepc (first column) and their corresponding optical strength (second column).

We can immediately notice two things: first, all the excitons found here are doubly degenerate. This is a consequence of the rotation symmetry of the hexagonal MoS2 crystal lattice.

Second, the first degenerate pair does not couple with light (a consequence of its spin-triplet structure): it’s a dark exciton. The excitons corresponding to the first two peaks seen in absorption are the (3-4) and (7-8), respectively.

Therefore, we will try to plot the wavefunction of excitons (3-4). Yambo will automatically recognize the degeneracy and sum the components accordingly.

To generate the ypp input file for the exciton wavefunction type

$ ypp -e w -F ypp_wfc.in

(as with yambo, you can see all the available options with ypp -h; here -e w stands for exciton wavefunction).

Open the resulting input file and modify the variables as shown. Try to think about the meaning of runlevels and variables as explained in the comments.

excitons                         # [R] Excitonic properties
wavefunction                     # [R] Wavefunction
Format= "x"                      # Output format [(c)ube/(g)nuplot/(x)crysden]
Direction= "123"                   # [rlu] [1/2/3] for 1d or [12/13/23] for 2d [123] for 3D
FFTGvecs=  80            Ry    # [FFT] Plane-waves
#NormToOne                     # Normalize to one the maximum value of the plot
States= "3 - 3"                  # Index of the BS state(s)
BSQindex= 1                      # Q-Index of the BS state(s)
Degen_Step= 0.010000       eV    # Maximum energy separation of two degenerate states
% Cells
 12 | 12 | 1 |                   # Number of cell repetitions in each direction (odd or 1)
%
% Hole
 1.475 | 2.555 | 1.468 |        # [cc] Hole position in unit cell (positive)
%

We have selected the third exciton state in the list of States. The Cells variable represents the extension in real space we want to consider in the calculation. In MoS2, excitons have a large Bohr radius so we need to use a large number of repeated unit cells.

Finally, the hole position \(\mathbf{r}_0\). We want to fix it in the middle between an Mo-S bond. How do we do that? Check again the previous *E_sorted file:

[...]
# Atom 1 with Z 42 [cc]:-0.295004043E-8   3.40641356      0.00000000
# Atom 1 with Z 16 [cc]:  2.95004058      1.70320678      2.93654299
# Atom 2 with Z 16 [cc]:  2.95004058      1.70320678     -2.93654299
[...]

These are the atomic positions in the unit cell in Cartesian coordinates. We can easily compute the midpoint between the first atom (Z=42, Mo) and the second (Z=16, S).

Finally, let’s submit the input with the script run_ypp.sh. It will create a new directory EXC_WF.

At the end of the calculation, in there you will find the output file o-EXC_WF4.exc_qpt1_3d_3.xsf. This can be visualized, for example, with the programs xcrysden or VESTA.

$ VESTA o-EXC_WF4.exc_qpt1_3d_3.xsf

You will see the atomic structure and the wavefunction intensity data represented as isosurface. After working on the figure layout, you should find something similar to this:

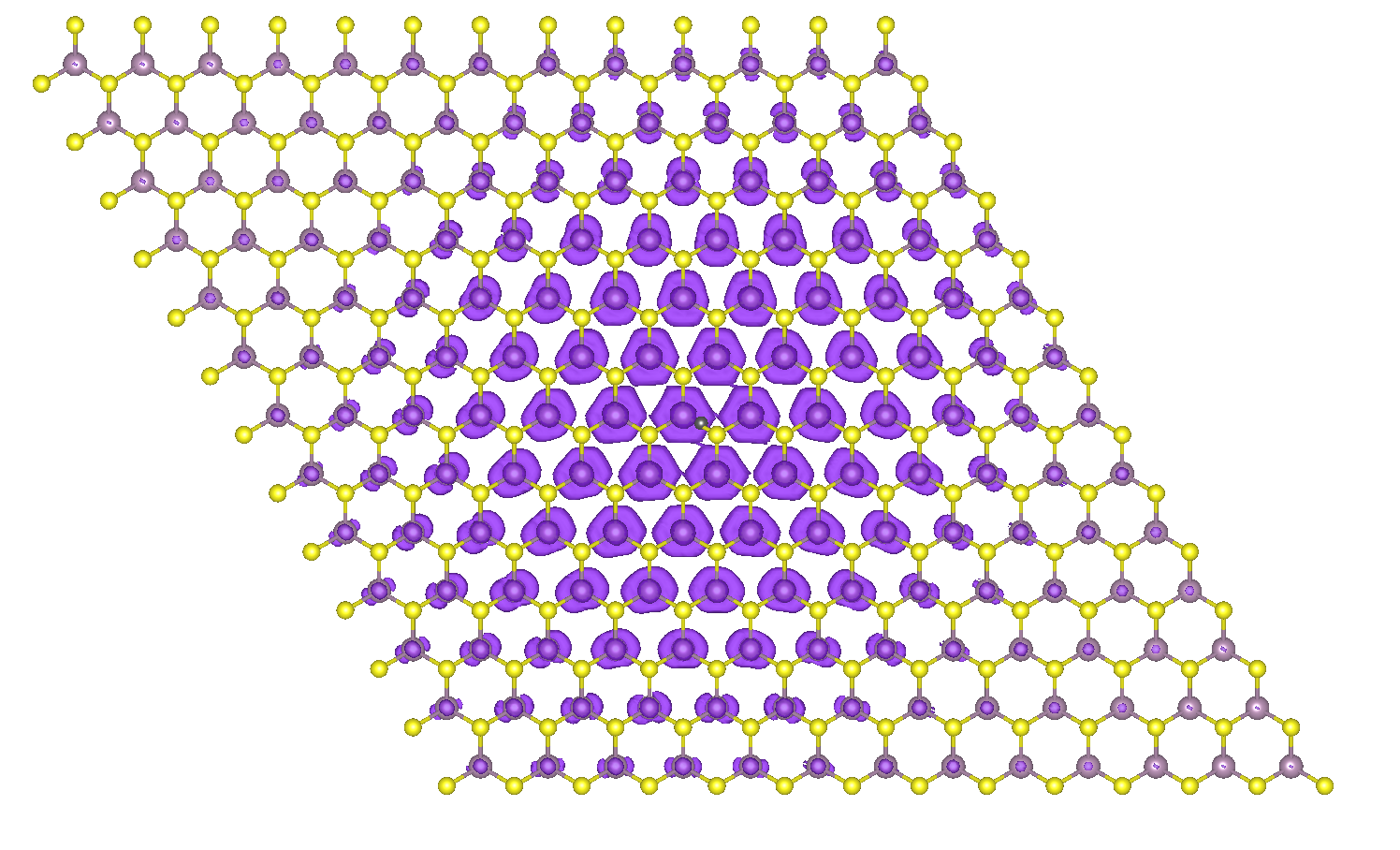
../../_images/MoS2-2D-excwf.png

Electron density distribution when hole is fixed between the Mo-S bond for the first bright exciton of monolayer MoS2.

Note that when the hole is fixed between a Mo-S bond, the relative eletron sits onto the Mo atoms. Try to inspect closely the shape of the isosurface on each atom: what does it remind you of? What does this shape suggest about the orbital character of the conduction electrons forming the bright exciton in MoS2?